I followed a tutorial on Convolutional Neural Networks that left many questions unanswered. Soon I realized that the actual process of architecting a Neural Network and setting the parameters seemed to be much more experimental than I thought. It took a while to find explanations that a rookie like me could understand. Most of the posts I found gloss over the difficult details, like what NN configuration to choose, or which library to choose, or why would you use ReLU in an image-recognition NN and focused on easier and more consistent tasks, like setting up a Python environment.
TL;DR
Keras allows you to build a neural network in about 10 minutes. You spend the remaining 20 hours training, testing, and tweaking.
If you wish to learn how a Convolutional Neural Network is used to classify images, this is a pretty good video.
The ultimate guide to convolutional neural networks honors its name.
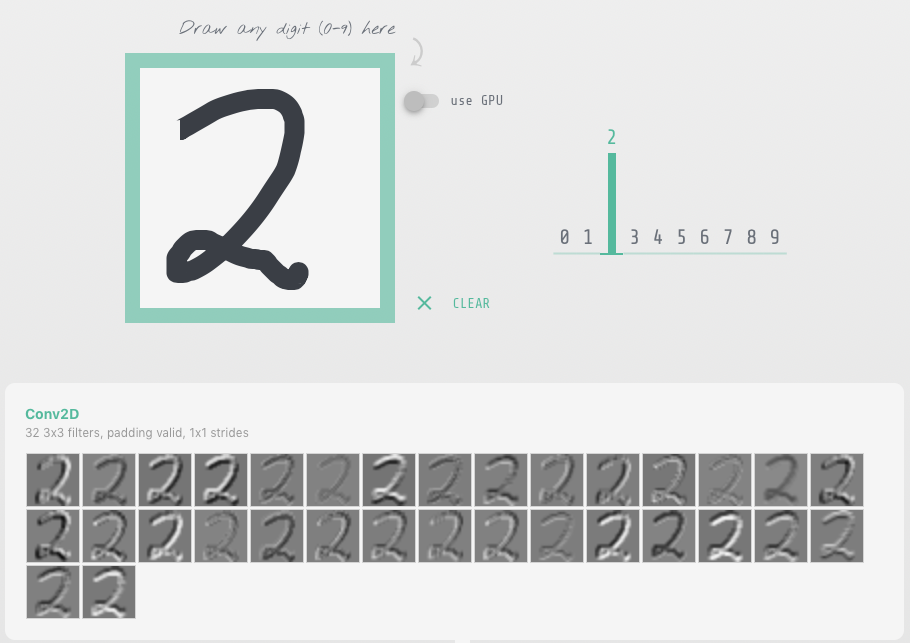
This example illustrates how a CNN recognizes numbers: Basic Convnet for MNIST
Get the code at https://github.com/danielpradilla/python-keras-fruits.
A simple problem
In order to learn the basics, I started a simple –um, “simple”– project to build a deep neural network to correctly classify a set of 17 kinds of fruits from the Kaggle Fruits 360 dataset.
Keras provides an easy interface to create and train Neural Networks, hiding most of the tedious details and allowing you to focus on the NN structure. It interfaces with the most popular NN frameworks: Tensorflow, CNTK, and Theano. This answered one of my first questions, “Keras vs Tensorflow, which one should you learn and when to use each one?” –short answer: learn Keras until you need Tensorflow.
Keras allows you to go from idea to working NN in about 10 minutes. Which is impressive. The Keras workflow looks like this:
- Get training and testing data
- Define the layers
- Compile the model
- Train model
- Evaluate the model
- Get predictions
Get training and testing data
Keras provides a neat file-system-based helper for ingesting the training and testing datasets. You create a “training” and “validation” folder, and put your images there. In the case of a multi-category classifier like this one, each image class will have their own folder –”Apple”, “Oranges”, etc. flow_from_directory() will automatically infer the labels from the directory structure of the folders containing images. Every subfolder inside the training-folder (or validation-folder) will be considered a target class.
Alternatively, you can ingest the data on your own and do a manual split.
flow_from_directory is a property of ImageDataGenerator, a generator class that offers a memory-efficient iterator object. When you have large datasets it’s always wise to use a generator that yields batches of training data. More info at “A thing you should know about Keras if you plan to train a deep learning model on a large dataset”

Remember that, even though we clearly see that this is an avocado, all the neural network may see is the result of some edge-detection filters. So an avocado is this apparently green oval thing placed in the middle of the field. If you train the NN with perfectly-centered avocados and then feed it an off-center avocado, you might get a poor prediction.
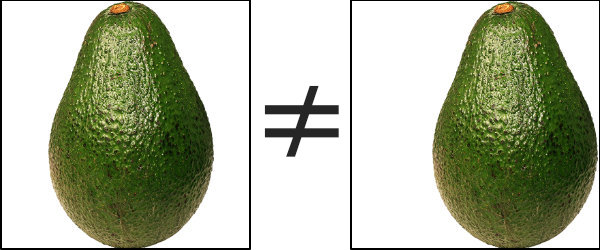
In order to account for this and facilitate the training process, Keras provides the ImageGenerator class, which allows you to define configuration parameters for augmenting the data by applying random changes in brightness, rotation, zoom, and skewing. This is a way to artificially expand the data set and increase the robustness of the training data.
One particularly important image augmentation step is to rescale the RGB values in the image to be within the [0,1] range, dividing each color value by 255. This normalizes the differences in pixel ranges across all images, and contributes to creating a network that learns the most essential features of each fruit. More info at Image Augmentation for Deep Learning with Keras.
test_gen = k.preprocessing.image.ImageDataGenerator( rotation_range=0.1, width_shift_range=0.1, height_shift_range=0.1, brightness_range=[0.5, 1.5], channel_shift_range=0.05, rescale=1./255 ) test_images_iter = test_gen.flow_from_directory(TEST_PATH, target_size = TARGET_SIZE, classes = VALID_FRUITS, class_mode = 'categorical', seed = SEED)
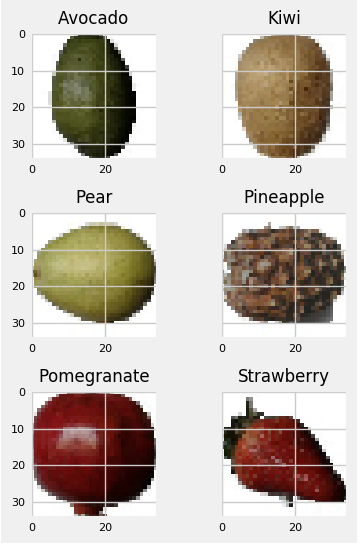
More image training data
There are a couple of datasets that are commonly used for training Neural Networks
COCO
CFAR
Network Architecture
What is the configuration of the Neural Network? How many convolutional layers, how many filters in each convolutional layer and what’s the size of these filters? These were some of the questions that arose as I started to read tutorials, papers, and documentation. Turns out that in the majority of the cases, the answer is “it depends”. It depends on the data, your previous decisions on image size, your goals in terms of accuracy/speed, and your personal understanding of what you deem a good solution.
Understanding Convolutional Neural Networks
This guide presents a high-level overview of the typical neural network structures that you can build in Keras: https://keras.io/getting-started/sequential-model-guide/
I watched a bunch of videos and this one provides the best explanation of what is a CNN and how it works:
The ultimate guide to convolutional neural networks honors its name. But the best way to understand how a CNN and each layer works at the most fundamental level is with these two examples:
Layers are the building blocks of Neural Networks, you can think of them as processing units that are stacked (or um layered) and connected. In the case of feed-forward networks, like CNNs, the layers are connected sequentially. Commonly, each layer is comprised of nodes, or “neurons”, which perform individual calculations, but I rather think of layers as computation stages, because it’s not always clear that each layer contains neurons.
The process of creating layers with Keras is pretty straightforward. Just call keras.layers and push them into a list.
The two questions I found the hardest to answer were How many layers do I have to set up? and What is the number of nodes in each one? These are often overlooked in tutorials because you are just following the decisions of someone else. I bet that in the coming months we will see an abstraction similar to Keras with which you won’t even have to think of the number of layers.
The easy layers to figure out are the input and output layers. The input layer has one input node and in Keras there is not need to define it. The output layer depends on the type of neural network. If it’s a regressor or a binary classifier, then it has one output –you are either returning a number or a true/false value. If it’s a multi-class classifier with a softmax function at the end, you will need one node per class –in our case, one per type of fruit we are attempting to classify.
rtn = k.Sequential() #input ##something?? rtn.add(k.layers.Dense(units = len(trained_classes))) #output
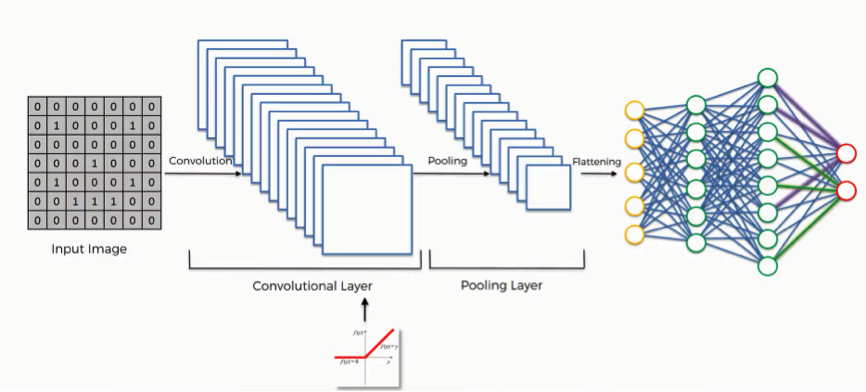
Now, for the hidden layers, we need to think about the structure of a Convolutional Neural Network. In general terms, Convolutional Neural Networks have two parts: a set of convolution layers and a set of fully connected layers. The convolution layers produce feature maps (mappings of activations of the different parts of an image), which are then pooled, flattened out and passed on to the fully connected layers.
source: https://www.superdatascience.com/blogs/the-ultimate-guide-to-convolutional-neural-networks-cnn
For the convolution layers, we need to strike a balance between performance and quality of the output. In this particular case, I noticed that having a single convolution already produced 97% accuracy, and I added an extra convolution because the convergence of the validation accuracy seemed smoother. Since all the images were of high quality –a rotation of a single fruit with transparent background– a single convolution would’ve done the job. I bet that there are cases with lower-quality images in which the extra convolutions will improve the performance of the network.
The best explanation that I found for convolutional layers is to imagine a flashlight sliding over areas of an image and capturing the data (1s and 0s) that is being made visible.
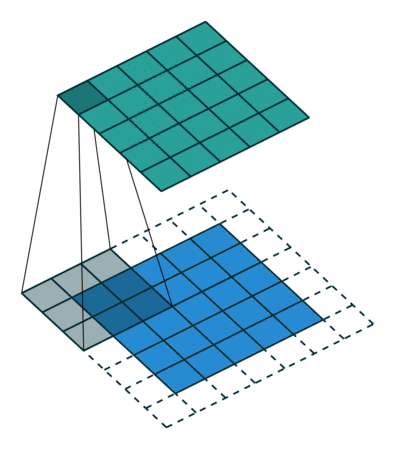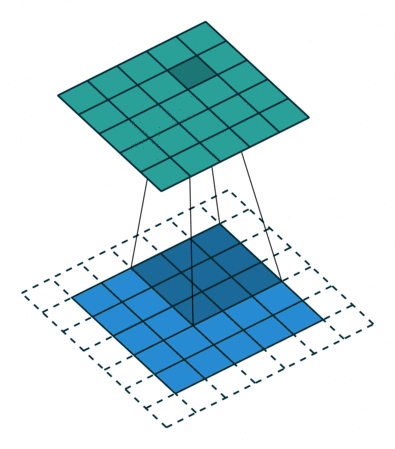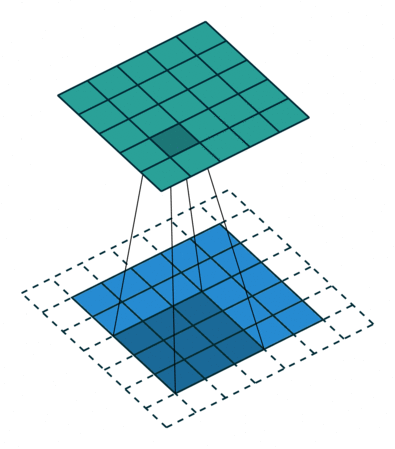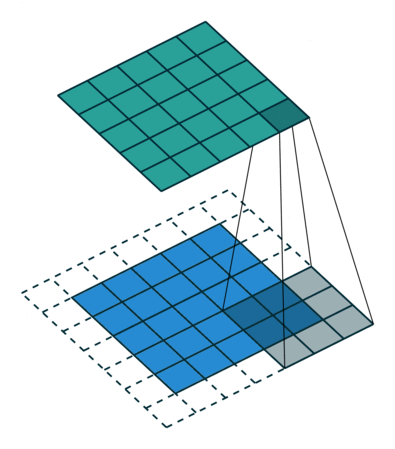
source: https://medium.com/syncedreview/a-guide-to-receptive-field-arithmetic-for-convolutional-neural-networks-42f33d4378e0
The flashlight is what we call a filter, the area that it is shining over is the receptive field and the way that the data is interpreted depends on weights and parameters. Each filter will have 1s and 0s arranged in a particular way, forming patterns that capture a particular feature, one filter will be pretty good at capturing straight lines, another one will be good at curves or checkered patterns. As the flashlight slides (convolves) the receptive field over the image, the values contained in the filter will be multiplied by the values contained in the image, creating what is called an activation map, a matrix that shows how a particular filter “activated” the information contained in the image.
The number of filters in the convolution is largely empirical. Common practice seems to be that, as you go deeper in the network, you learn more features, so you add more filters to each successive convolutional layer. I started with 16 and 32 for the next layer and then observed better results by switching to 32/64 and then to 64/128. These are single-fruit images with a blank background. A more complex dataset might require a larger number of filters, or more layers.
The kernel_size must be an odd integer. What I’ve seen most is 3×3 for small images (less than 128 pixels in size) or 5×5 and 7×7 for larger images.
I left striding at 1, but you may increase it if you need to reduce the output dimensions of the convolution.
I set padding to “same” to keep the output size of the convolution equal to the input size.
I used L2 kernel regularization and drop-off because that’s what I read I should do to reduce overfitting.
#first convolution rtn.add(k.layers.Conv2D(filters = 64, kernel_size = (3,3), padding = 'same', strides=(1, 1), input_shape = (IMG_WIDTH, IMG_HEIGHT, CHANNELS), kernel_regularizer=k.regularizers.l2(0.0005), name='conv2d_1')) #second convolution rtn.add(k.layers.Conv2D(filters = 128, kernel_size = (3,3), padding = 'same', name='conv2d_2'))
I read many guides using Dropout in between convolution layers for reducing overfitting. The Dropout algorithm randomly sets some of the layer’s values to 0, in order to force the network to learn new paths for representing the same data.
I read that Dropout is most effective as a regularization method in the fully connected portion of the NN. For the convolution, two methods are available, Spatial Dropout and Batch Normalization. From the Keras documentation, we can learn that Spatial Dropout seems to be the dropout method to use between convolution layers:
“If adjacent pixels within feature maps are strongly correlated (as is normally the case in early convolution layers) then regular dropout will not regularize the activations and will otherwise just result in an effective learning rate decrease”
For the activations, I used Rectified Linear Unit. ReLU is ideal for enhancing the transitions between pixels (edges, changes in colors). I also used Leaky ReLU (paper) to avoid the dying ReLU problem. In case you need to do some kind of visual recognition. ReLU and Leaky ReLU seem to perform better than the traditional sigmoid function used in neural networks.
At the end of all the convolutions, we insert a pooling layer, which down-samples the feature maps and reduces the dimensionality of the problem. Pooling takes the maximum value of a sliding receptive field over each feature map. It also helps make the detection of certain features invariant to scale and orientation. In other words, it makes the network more robust by focusing on the most important features of the image.
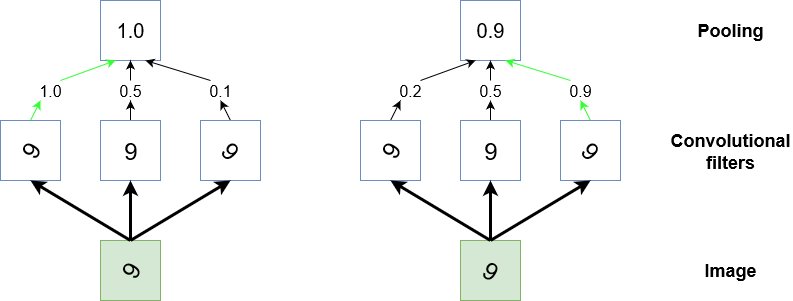
source: https://adventuresinmachinelearning.com/convolutional-neural-networks-tutorial-tensorflow/
After the pooling layer, we flatten the resulting matrix into a vector and we feed it through a fully-connected network. Each element in this vector will correspond to one or more features detected in the convolution, and the purpose of this fully-connected layers is to make classifications. In other words, after the convolution, we staple a standard neural network classifier. At the tail end, the fully-connected network will produce a probability distribution per each class, and these distributions will depend on the weight attributed to each neuron in the final classification. Though back propagation, Keras will automatically adjust the weight of each of these connections in order to minimize the classification error.
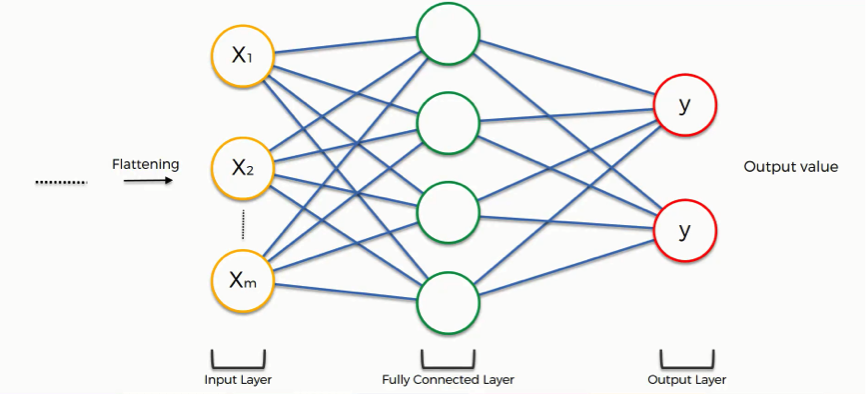
The key decision point at this stage will be the number of units that each layer of the fully connected network will have. This section of the comp.ai.neural-nets FAQ discusses the issue at length. I take away this part:
“For a noise-free quantitative target variable, twice as many training cases as weights may be more than enough to avoid overfitting. For a very noisy categorical target variable, 30 times as many training cases as weights may not be enough to avoid overfitting. An intelligent choice of the number of hidden units depends on whether you are using early stopping or some other form of regularization. If not, you must simply try many networks with different numbers of hidden units, estimate the generalization error for each one, and choose the network with the minimum estimated generalization error.”
This sample is relatively low noise and, after much repetition, I found an ok-performing network with 250 units.
# flatten into feature vector
rtn.add(k.layers.Flatten())
# output features onto a dense layer
#rtn.add(k.layers.Dense(units = len(trained_classes_labels) * 20, name='dense_1' ) )
rtn.add(k.layers.Dense(units = 250, name='dense_1' ) )
rtn.add(k.layers.Activation('relu', name='activation_dense_1'))
# randomly switch off 50% of the nodes per epoch step to avoid overfitting
rtn.add(k.layers.Dropout(0.5))
# output layer with the number of units equal to the number of categories
rtn.add(k.layers.Dense(units = len(trained_classes_labels), name='dense_2'))
rtn.add(k.layers.Activation('softmax', name='activation_final'))
Visualizing the network architecture
I was going to put here a really cool visualization of the network, but quickly found out that that’s a whole other area of research and experimentation. I’ll leave it for a future post. This is the output of model.summary()
Layer (type) Output Shape Param # ================================================================= conv2d_1 (Conv2D) (None, 35, 35, 64) 1792 _________________________________________________________________ batch_normalization_3 (Batch (None, 35, 35, 64) 256 _________________________________________________________________ activation_conv2d_1 (Activat (None, 35, 35, 64) 0 _________________________________________________________________ spatial_dropout2d_2 (Spatial (None, 35, 35, 64) 0 _________________________________________________________________ conv2d_2 (Conv2D) (None, 35, 35, 128) 73856 _________________________________________________________________ batch_normalization_4 (Batch (None, 35, 35, 128) 512 _________________________________________________________________ activation_conv2d_2 (LeakyRe (None, 35, 35, 128) 0 _________________________________________________________________ max_pooling2d_2 (MaxPooling2 (None, 17, 17, 128) 0 _________________________________________________________________ flatten_2 (Flatten) (None, 36992) 0 _________________________________________________________________ dense_1 (Dense) (None, 250) 9248250 _________________________________________________________________ activation_dense_1 (Activati (None, 250) 0 _________________________________________________________________ dropout_2 (Dropout) (None, 250) 0 _________________________________________________________________ dense_2 (Dense) (None, 17) 4267 _________________________________________________________________ activation_final (Activation (None, 17) 0 ================================================================= Total params: 9,328,933 Trainable params: 9,328,549 Non-trainable params: 384 _________________________________________________________________
Compilation
After we define our network architecture, we can compile the model using model.compile
For the loss function, I used categorical-cross-entropy because this is a multi-class classification problem. Binary-cross-entropy would be the one in a binary classification problem and mean-squared-error for a regression.
Regarding the optimizer, RMSprop is the recommended one in the Keras documentation, although I see many people using Adam. I actually tested with Adam and it seemed to converge quicker, but then the accuracy degraded on each epoch.
my_model.compile(loss = 'categorical_crossentropy', metrics = ['accuracy'], optimizer = k.optimizers.RMSprop(lr = 1e-4, decay = 1e-6) )
Fitting
This is the step which actually generates the model. There are two functions which you can use to fit a model in Keras.
- fit loads the whole dataset in memory
- fit_generator feeds off a generator and it’s intended for large datasets
I will use fit_generator in this example because i’m using an iterator (flow_from_directory) to load the images.
The fit process runs a full cycle of training and testing multiple times. Each of this runs is called an epoch. After each epoch we can measure the accuracy and loss of the model. If we run a backward propagation algorithm, we can minimize the error of the model using gradient descent on each successive epoch. The number of samples used for the gradient descent calculation is specified with the batch_size parameter. Keras automatically runs the back propagation algorithm for you and adjusts the weights. After each run, you can instruct Keras to run certain commands, like for example saving a model checkpoint with the current weights.
“For computational simplicity, not all training data is fed to the network at once. Rather, let’s say we have total 1600 images, we divide them in small batches say of size 16 or 32 called batch-size. Hence, it will take 100 or 50 rounds(iterations) for complete data to be used for training. This is called one epoch, i.e. in one epoch the networks sees all the training images once”
The fit_generator returns a history object with 4 measures: training loss, training accuracy, validation loss and validation accuracy. The training metrics are a comparison of the output of the model with the training images and the validation metrics are a comparison with the test or validation images (the ones not used for training).
Since you want to know how good your model is generalizing, you should focus on the validation metrics. Each epoch constitutes a complete training and validation cycle and Keras provides an automated way of saving the best results of all the epochs with the ModelCheckpoint callback.
start = dt.now()
history = my_model.fit_generator(
# training data
train_images_iter,
# epochs
steps_per_epoch = train_images_iter.n // BATCH_SIZE, #floor per batch size
epochs = EPOCHS,
# validation data
validation_data = test_images_iter,
validation_steps = test_images_iter.n // BATCH_SIZE,
# print progress
verbose = 1,
callbacks = [
#early stopping in case the loss stops decreasing
k.callbacks.EarlyStopping(monitor='val_loss', patience=3),
# only save the model if the monitored quantity (val_loss or val_acc) has improved
k.callbacks.ModelCheckpoint("fruits_checkpoints.h5", monitor='val_loss', save_best_only = True),
# only needed for visualising with TensorBoard
k.callbacks.TensorBoard(log_dir = "logs/{:%d_%b_%Y_%H:%M:%S}".format(dt.now()) )
]
)
Evaluate the model
I followed the Keras docs on model visualization to generate the accuracy and loss plots.
You can also use TensorBoard, which offers an easy way to compare multiple runs with different parameters.
Plotting is very useful as it allows you to see whereas the model is undefitting or overfitting. Underfitting, or under-learning is pretty easy to spot: the training lines don’t converge as expected (to 0 loss or 100% accuracy). Overfitting is a little bit trickier. For such a clean dataset, any sudden changes in the validation line is a sign of overfitting. If the accuracy stops improving is also a sign of overfitting, this is when the early stopping feature might become handy.
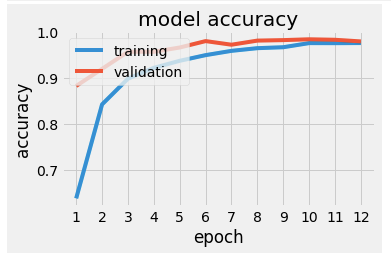
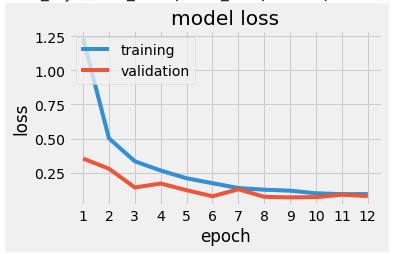
In this case, I tried to smooth the lines for loss and accuracy by introducing and tweaking dropout and batch normalization.
Predictions
Once we have our fitted model, we can feed an image to the predict method and get a list of probabilities of the image belong to each class. We can also use the predict_classes method to get the label of the most probable class.
In order to feed the image to the predict method, you will need to load it and convert it to an array –remembering to divide it by 255 to normalize the channels.
loaded_image = k.preprocessing.image.load_img(path=PREDICTION_PATH+'/'+filename, target_size=(IMG_WIDTH,IMG_HEIGHT,CHANNELS)) #convert to array and resample dividing by 255 img_array = k.preprocessing.image.img_to_array(loaded_image) / 255. #add sample dimension. the predictor is expecting (1, CHANNELS, IMG_WIDTH, IMG_HEIGHT) img_np_array = np.expand_dims(img_array, axis = 0) #img_class = my_model.predict_classes(img_np_array) predictions = my_model.predict(img_np_array)
I downloaded a bunch of images from the internet, taking care of finding some with the same orientation as the training and testing images. I wasn’t expecting this neural network to do magic. I put all the images in the same folder and ran the prediction code in a loop.
Can we recognize an avocado? Yes!
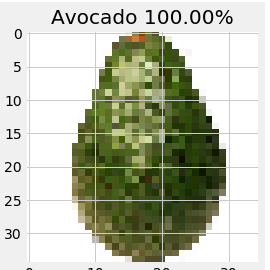
How about a pomegranate –this one is tricky, because its round shape is shared with many fruits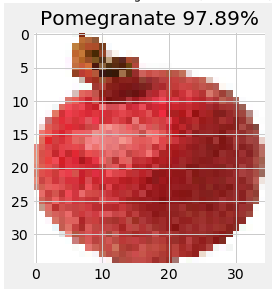
A pear?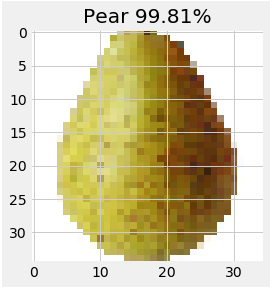
A kiwi?
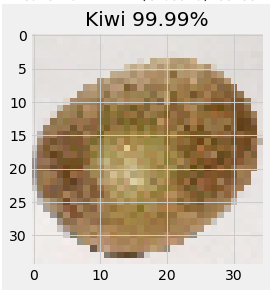
A sliced kiwi? Guess where the error comes from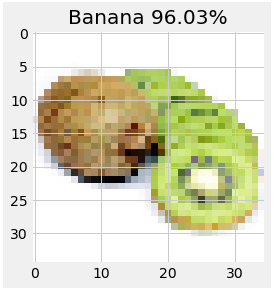
A kiwi, the animal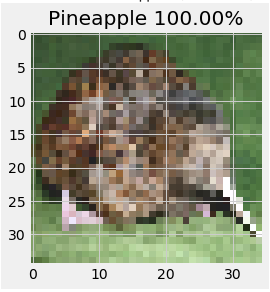
A pineapple?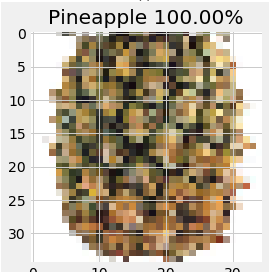
The network thinks that this other pineapple is a strawberry. This is because the training and testing images only have pineapples without leaves.
Speaking of strawberries:
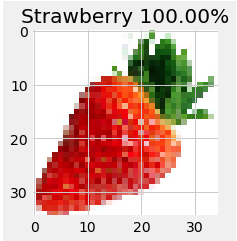
How about a drawing of a strawberry?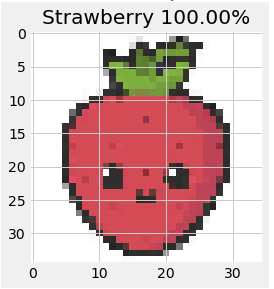
Is Strawberry Shortcake a strawberry? You bet!
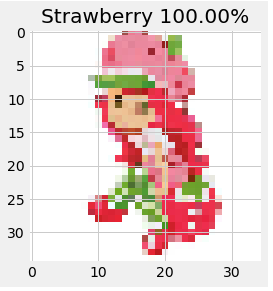
Ok that last one is maybe a fluke. Or is it? The features of a strawberry are definitely there.
Gratuitous “What does the network see?” images
These were made with the Keras Visualization Toolkit
Saliency
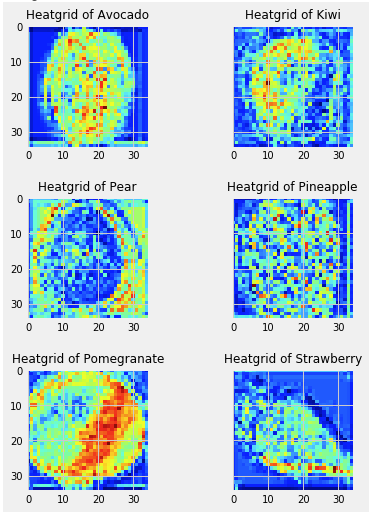
Activation maps
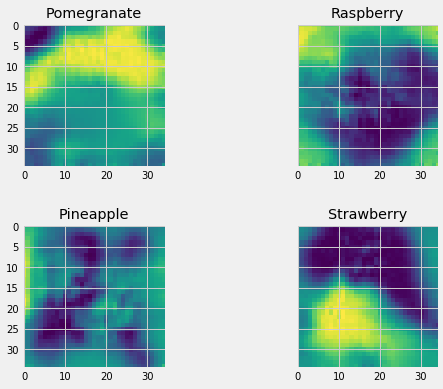
Some additional things I learned
Reading the tutorials one would think that the architecture of the network needs to be though out in advance. I discovered that there might be a lot of tweaking and back-and-forth involved. This also implies a lot of waiting for the training steps. These were –approximately– all the iterations of my network
Conv(16) -> Pooling -> Flatten -> Dense (100) -> Dense (17) Conv(32) -> Pooling -> Flatten -> Dense (100) -> Dense (17) Conv(32) -> SpatialDropout-> Conv(64) -> Pooling -> Flatten -> Dense (100) -> Dropout(0.5) -> Dense (17) Conv(32) -> SpatialDropout-> Conv(64) -> BatchNormalization-> Pooling -> Flatten -> Dense (100) -> Dropout(0.5) -> Dense (17) Conv(32) -> BatchNormalization -> SpatialDropout-> Conv(64) -> BatchNormalization-> Pooling -> Flatten -> Dense (300) -> Dropout(0.5) -> Dense (17) Conv(64) -> BatchNormalization -> SpatialDropout-> Conv(128) -> BatchNormalization-> Pooling -> Flatten -> Dense (250) -> Dropout(0.5) -> Dense (17)
I also found out that tensorflow-gpu currently only runs on CUDA-enabled NVIDIA GPUs, so no luck with my current Macbook –yes, maybe you can hack something with OpenCL, but if you are going down that route, just switch the underlying Keras library from Tensorflow to Theano.
One of my mistakes was that I was applying too much dropout, effectively making my model underfit. I was applying too many corrective measures to a problem I didn’t have, yet. I should’ve started the other way around: overfitting the model, then take measures against overfitting.
I’ve seen a lot of beautiful TensorBoard visualizations, but if you build your models with Keras and you don’t explicitly create scopes, expect a very messy network graph.
Speaking about being messy, it is helpful to have some ideas on how to structure code and “proper” software engineering. This applies in almost any situation in Data Science, but specially in cases like this in which you perform a lot of recurring experiments.
I was confused when I trained my first model and saw that the testing accuracy was higher than the training accuracy –and the training loss much higher than the testing loss. Intuition points to the contrary. How is that possible?
From the Kears FAQ:
“A Keras model has two modes: training and testing. Regularization mechanisms, such as Dropout and L1/L2 weight regularization, are turned off at testing time.
Besides, the training loss is the average of the losses over each batch of training data. Because your model is changing over time, the loss over the first batches of an epoch is generally higher than over the last batches. On the other hand, the testing loss for an epoch is computed using the model as it is at the end of the epoch, resulting in a lower loss.”
Meaning: that behavior is normal.
You can get the complete code for this post at https://github.com/danielpradilla/python-keras-fruits